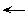Table of Contents Watch What I Do
Writing static language statements interspersed with compile-run-debug-edit periods is obviously a poor way to communicate. Suppose two humans tried to interact this way! Specifically, it is poor because it is:
So why aren't interactive languages more widely used? Most are high level languages that are not as efficient as low level ones such as C and FORTRAN. In their search of a competitive advantage, software developers want their programs to execute as fast as possible, even at the expense of a longer development time. But this situation may be changing. Computers are now fast enough that interactive languages are practical in some cases. Several commercial applications have been written in Lisp, and IBM now recommends Smalltalk for developing applications under its OS/2 operating system. Even some versions of C now contain an interpreter for quick development and debugging.
One
of the advantages of analogical representations over Fregean ones is that
structures and actions in a context using analogical representations (a
"metaphorical" context) have a functional similarity to structures and actions
in the context being modeled. One can discover relationships in a metaphorical
context that are valid in the other context. For example, there are five items
in array A; triangles have three sides; bicycles have two wheels; Texas is in
the south. Analogical representations suggest operations to try, and it is
likely that operations applied to analogical representations would be legal in
the other context, and vice versa. This is the philosophical basis for the
design of the Xerox Star and, ultimately, Apple Macintosh "desktop" user
interfaces; they are a metaphor for the physical office [Smith 82]. Being able
to put documents in folders in a physical office suggests that one ought to be
able to put document icons in folder icons in the computer "desktop," and in
fact one can.
Jerome Bruner, in his pioneering work on education [Bruner 66], identified three ways of thinking, or "mentalities":
Jacques Hadamard, in a survey of mathematicians [Hadamard 45], found that many mathematicians and physicists think visually and reduce their thoughts to words only reluctantly to communicate with other people. Albert Einstein, for example, said that "The words of the language, as they are written or spoken, do not seem to play any role in my mechanism of thought. The psychical entities which seem to serve as elements in thought are certain signs and more or less clear images which can be `voluntarily' reproduced and combined.... This combinatory play seems to be the essential feature in productive thought--before there is any connection with logical construction in words or other kinds of signs which can be communicated to others.... The above mentioned elements are, in my case, of visual and some of muscular type. Conventional words or other signs have to be sought for laboriously only in a secondary stage, when the mentioned associative play is sufficiently established and can be reproduced at will." [Hadamard 45, pp.142-3]
Some things are difficult to represent analogically, such as "yesterday" or "a variable-length array." But for concepts for which they are appropriate, analogical representations provide an intuitively natural paradigm for problem solving, especially for children, computer novices, and other ordinary people. And a convincing body of literature suggests that analogical representations, especially visual images, are a productive medium for creative thought [Arnheim 71].
Words are Fregean. Yet words and rather primitive data structures are often the only tools available to programmers for solving problems on computers. This leads to a translation gap between the programmer's mental model of a subject and what the computer can accept. I believe that misunderstanding the value of analogical representations is the reason that almost all so-called visual programming languages, such as Prograph, fail to provide an improvement in expressivity over linear languages. Even in these visual languages, the representation of data is Fregean.
With the advent of object-oriented programming, the data structures available have become semantically richer. Yet most objects are still Fregean. A programmer must still figure out how to map, say, a fish into instance variables and methods, which have nothing structurally to do with fish.
What's needed is a lightweight, non-threatening medium like the back of a napkin, wherein one can sketch and play with ideas. The computer program described in the remainder of this chapter, Pygmalion, was an attempt to provide such a medium. Pygmalion was an attempt to allow people to use their enactive and iconic mentalities along with the symbolic in solving problems.
This urge to create something living is common among artists. Michelangelo is said to have struck with his mallet the knee of perhaps the most beautiful statue ever made, the Pieta, when it would not speak to him. And then there's the story of Frankenstein. Artists have consistently reported an exhilaration during the act of creation, followed by depression when the work is completed. "For it is then that the painter realizes that it is only a picture he is painting. Until then he had almost dared to hope that the picture might spring to life." (Lucien Freud, in [Gombrich 60], p.94) This is also the lure of programming, except that unlike other forms of art, computer programs do "come to life" in a sense.
The Pygmalion described in this chapter is a computer program that was designed to stimulate creative thinking in people [Smith 75]. Its design was based on the observation that for some people blackboards (or whiteboards these days) provide significant aid to communication. If you put two scientists together in a room, there had better be a blackboard in it or they will have trouble communicating. If there is one, they will immediately go to it and begin sketching ideas. Their sketches often contribute as much to the conversation as their words and gestures. Why can't people communicate with computers in the same way?
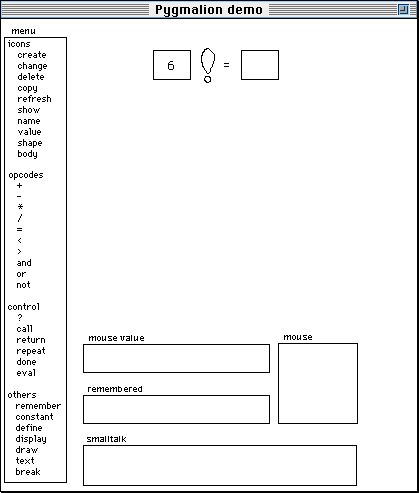
Pygmalion is a two-dimensional, visual programming environment implemented on an interactive computer with graphics display. (Although this work was completed nearly two decades ago, I will describe it in the present tense for readability.) It is both a programming language and a medium for experimenting with ideas. Communication between human and computer is by means of visual entities called "icons," subsuming the notions of variable, data structure, function and picture. Icons are sketched on the display screen. The heart of the system is an interactive "remembering" editor for icons, which both executes operations and records them for later reexecution. The display screen is viewed as a picture to be edited. Programming consists of creating a sequence of display images, the last of which contains the desired information. Display images are modified by graphical editing operations.
In the Pygmalion approach, a programmer sees and thinks about a program as a series of screen images or snapshots, like the frames of a movie. One starts with an image representing the initial state and transforms each image into the next by editing it to produce a new image. The programmer continues to edit until the desired picture appears. When one watches a program execute, it is similar to watching a movie. The difference is that, depending on the inputs, Pygmalion movies may change every time they are played. One feature that I didn't implement but wish I had is the ability to play movies both backward and forward; then one could step a program backward from a bug to find where it went wrong.
There are two key characteristics of the Pygmalion approach to programming.
Another early attempt to specify programming by editing was Gael Curry's Programming by Abstract Demonstration [Curry 78]. It was similar to Pygmalion, except that instead of dealing with concrete values, Curry manipulated abstract symbolic representations (e.g. "n") for data. While this made some things easier to program than in Pygmalion, it is interesting to note that in his thesis he reported making exactly the kinds of boundary errors mentioned above because he could not see actual values.
integer function factorial (integer n) =
if n = 1 then 1
else n
* factorial(n - 1);
In Pygmalion, a person would define factorial by picking some number, say "6", and then working out the answer for factorial(6) using the display screen as a "blackboard." In the illustrations below, in order to save space I won't show the entire display screen for each "movie frame." Rather, I'll often "zoom in" on the parts of the screen that change from frame to frame. The programmer, however, always sees the entire screen:
(Aside:
the screen shots in this chapter are from a recent HyperCard simulation of
Pygmalion done on a Macintosh computer by Allen Cypher and myself.
Therefore the window appearance differs slightly from the actual system.)
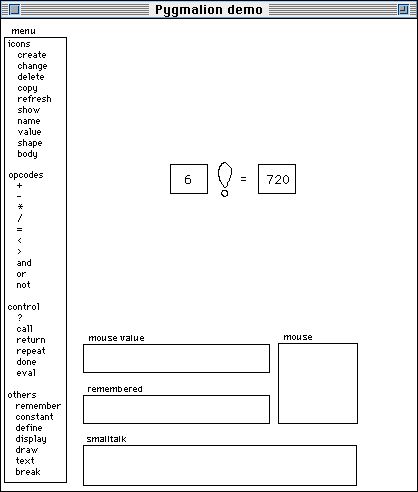
The Pygmalion window consists of several parts:
The entities with which one programs in Pygmalion are what I call "icons." An icon is a graphic entity that has meaning both as a visual image and as a machine object. Icons control the execution of computer programs, because they have code and data associated with them, as well as their images on the screen. This distinguishes icons from, say, lines and rectangles in a drawing program, which have no such semantics. Pygmalion is the origin of the concept of icons as it now appears in graphical user interfaces on personal computers. After completing my thesis, I joined Xerox's "Star" computer project. The first thing I did was recast the programmer-oriented icons of Pygmalion into office-oriented ones representing documents, folders, file cabinets, mail boxes, telephones, wastebaskets, etc. [Smith 82]. These icons have both data (e.g. document icons contain text) and behavior (e.g. when a document icon is dropped on a folder icon, the folder stores the document in the file system). This idea has subsequently been adopted by the entire personal computer and workstation industry.
To get started, I define an icon for the function:
I
create two sub-icons to hold the argument and value, and then draw some (crude)
graphics to indicate the icon's purpose:
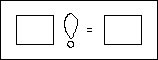
Finally
I make the outside border invisible:
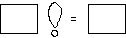
I
now select the icon, invoke the "define" operation, and type in the name
"factorial." This associates a name with the icon. The first thing the system
does with a newly created function is to capture the screen state. Whenever the
function is invoked, it restores the screen to this state. This is so that the
function will execute the same way regardless of what is on the screen when it
is called. So before invoking "define," I make sure that I clear off any
extraneous icons lying around. Icons may be deliberately left on the screen
when a function is defined; these act as global variables. When the function is
invoked, the "global" icons and their current values are restored to the screen
(if they weren't already present) and are therefore available to the
function.
As soon as I invoke the "define" operation, the system enters "remember mode," causing every action I subsequently do to be recorded in a script attached to the icon. So one defines functions simply by working out examples on the screen. Programs are created as a side effect. Here I'll arbitrarily work out the value of factorial for the number "6". (Choosing good examples is an art. One wants both typical values and boundary cases. Even in conventional programming, choosing test cases poorly is a principal sources of bugs. Pygmalion does not solve this problem.)
I type "6" into the argument icon:
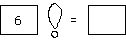
Whenever
all the arguments to a function are filled in, the system immediately invokes
it. This was an experiment and is not inherent in programming by demonstration,
or even necessarily a good idea. Functions in Pygmalion can be invoked
even if their code is undefined or incomplete. When the system reaches a part
of the function that has not yet been defined, it traps to the user asking what
to do next. This was implemented by placing a "trap" operator at the
end of every code script. When a trap operator is executed, the system reenters
"record mode." Every action subsequently performed is inserted in the code
script in front of the trap. When the user invokes the "done" operation
indicating that this code script is finished, the system leaves "record mode"
and removes the trap operator. Otherwise the trap operator remains there.
Factorial is now ready to execute, so the system invokes it. Since there is no code defined for it yet, it immediately traps to the programmer asking what to do. I move the factorial icon out of the way to make some room on the screen:
From
here on, in order to save space in these pictures I won't show the window title
or any area that is not directly involved in the actions being described.
I want to test if the argument is equal to 1. Actually, I can see that it isn't 1; it's 6. So why do I have to make a test? The answer is that Pygmalion is designed for programmers. Programmers know that functions will be called with different arguments, and they try to anticipate and handle those arguments appropriately. This is a little schizophrenic of Pygmalion: on the one hand it attempts to make programming accessible to a wider class of users; on the other, it relies on the kind of planning which only experienced programmers are good at. But anticipation is not inherent in programming by demonstration. Henry Lieberman's Tinker [Lieberman 80, 81, 82] doesn't force users to anticipate future arguments. In Tinker one writes code dealing only with the case at hand. When Tinker detects an argument that is not currently handled, it asks the programmer for a predicate to distinguish the new case from previous ones. The programmer then writes code to handle the new case. Tinker synthesizes a conditional expression from the predicate, the new code, and the existing code. Programmers never have to anticipate; they need only react to the current situation. This is an improvement over Pygmalion's approach.
At any rate, I've decided that I will need a conditional, so I invoke the "?" item in the menu. The system enters a mode waiting for me to specify where to put the conditional icon. When I click the mouse, the icon is placed at the cursor location:
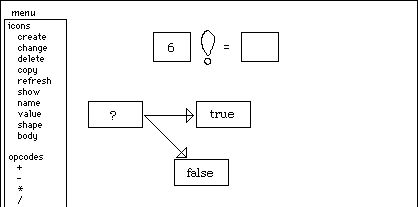
The
conditional icon consists of three sub-icons: one for the predicate and two to
hold the code for the true and false branches. The predicate icon is the
"argument" to the conditional; as soon as it has a value, the appropriate
branch icon executes.
To test if the factorial argument is equal to 1, I click on the "=" menu item, point where I want the icon to go, and the system creates an equality-testing icon:
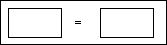
It
has two sub-icons to hold the data being tested. I drag the "6" down from
factorial's argument icon and deposit it in the left hand sub-icon:
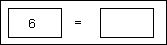
(During
playback--"watching the movie,"--Curry's system animated such value dragging,
making for a quite articulate movie; this was an improvement over
Pygmalion, which did no such animation.) Then I type a "1" into the
right hand sub-icon:
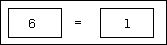
The
equality icon is now fully instantiated, so it executes. It is defined to
replace its contents with the result of the test. Since 6 is not equal to 1, it
replaces its contents with the symbol "false":
This
value, like the value in any icon on the screen, can be used in other parts of
the computation. In particular, it can be used in the conditional icon. I drag
it into the conditional's predicate icon. The conditional icon is now fully
instantiated, so it executes. The symbol "false" causes the false icon to be
evaluated:
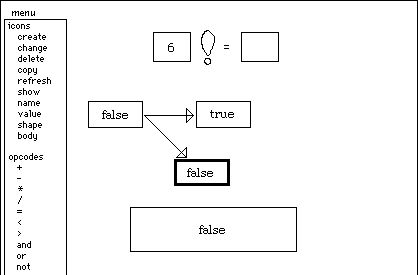
But
the false icon has no code defined for it yet, so it immediately traps back to
me asking what to do. The false icon now becomes the "remembering" icon;
previously it was the icon for factorial itself. So now I'm no longer defining
code for the factorial icon; I'm defining code for the false branch of its
conditional icon. In fact, from here on out all of the operations I perform
will be attached to either the true or false branch of the conditional.
Since I don't need the equality testing icon anymore, I'll get rid of it. I do this by invoking the "delete" menu item and then clicking on the equality icon.
Now I want to compute n*factorial(n-1). I'll need a multiplication icon and a subtraction icon. These I get by invoking the appropriate menu items:
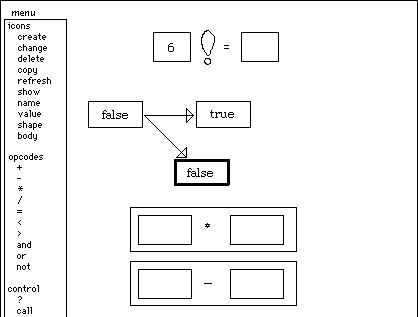
I
drag factorial's argument (6) into the left hand icon in each of these. Then I
type a 1 into the right hand icon in the subtracter:
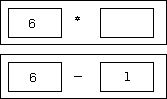
The
subtraction icon is now fully instantiated, so it executes:
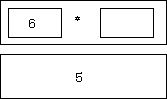
Now
I want to call factorial recursively on this value (5). I invoke the "call"
menu item, type "factorial" when prompted, and click where I want it to go. The
system creates a new instance of the factorial icon, the very one that I am in
the middle of defining! As mentioned earlier, that factorial is not completely
defined poses no problems for Pygmalion; it will execute what it has and
ask for more when it runs out. The screen now looks like this:
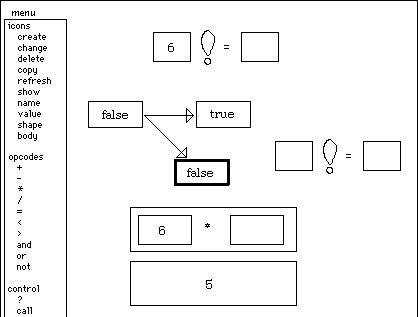
I
drag the 5 into factorial's argument icon. As usual since it is now fully
instantiated, it executes. But now instead of being empty, there is quite a bit
of code for factorial to execute:
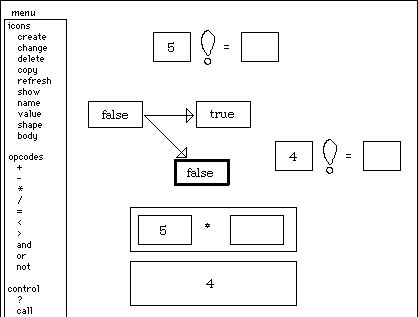
And so on recursively, until finally factorial is called with 1 as the argument. At this point, for the first time, the conditional's true icon is executed. But there is no code yet for this icon, so it immediately traps back to me asking for instructions. The screen now looks like this:
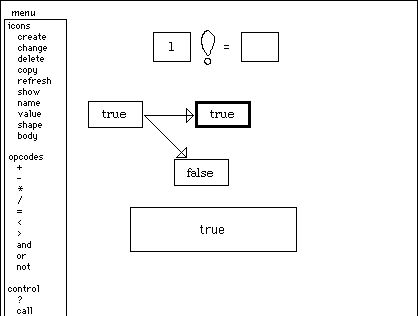
In
this case, we know exactly what to do. Factorial(1) = 1. So I type 1 into the
value icon:
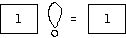
and
invoke the "done" menu item. This returns from the last recursive
call--factorial(1). It immediately traps asking for more instructions for the
false branch of the conditional, since it was still trying to compute
factorial(2) when the recursive call to factorial(1) was made. The screen now
looks like this:
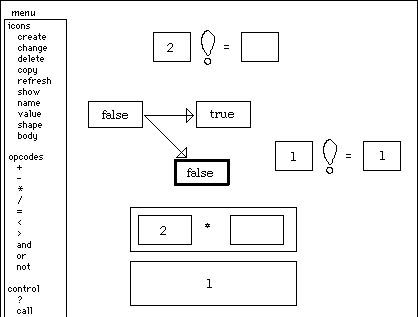
All
that remains is to drag the value from the recursive call factorial(1) into the
multiplication icon:
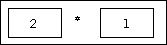
which
causes it to evaluate:
This
then is n*factorial(n-1), where n = 2. I drag this value into
factorial's value icon--the false branch as well as the true branch must
compute a value--and invoke "done."
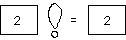
The
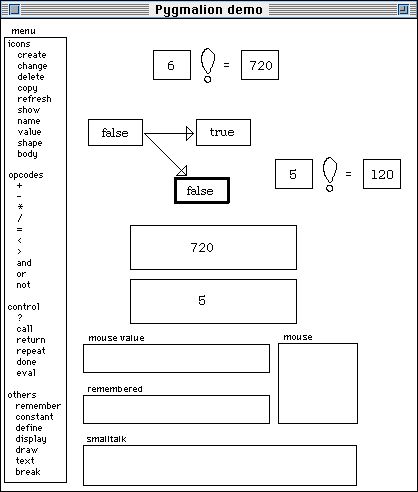
recursion now completely unwinds, since it knows how to do everything it needs
to, and ends with the value of factorial(6). See the next page. Finally, in the
picture on the following page, it restores the screen to its state when the
function was initially invoked.
1. The most important change I'd make is to address a broader class of users. Pygmalion was designed for a specific target audience: computer scientists. These people already know how to program, and they understand programming concepts such as variables and iteration. I would like to see if the approach could be applied to a wider audience: business people, homemakers, teachers, children, the average "man on the street." This requires using objects and actions in the conceptual space of these users: instead of variables and arrays, use documents and folders, or cars and trucks, or dolls and doll houses, or food and spices. Or better yet, let users define their own objects and actions. Dan Halbert captured this idea nicely with his concept of "programming in the language of the user interface" [Halbert 84].
2. The biggest weakness of Pygmalion, and of all the programming by demonstration systems that have followed it to date, is that it is a toy system. Only simple algorithms could be programmed. Because of memory limitations, I could execute factorial(3) but factorial(4) ran out of memory. (Pygmalion was implemented on a 64 K byte computer with no virtual memory.) There was no way to write a compiler in it or a chess playing program or an accounting program, nor is it clear that its approach would even work for such large tasks. (I did, however, implement part of an operating system in it, at least on paper.) The biggest challenge for programming by demonstration efforts is to build a practical system in which nontrivial programs can be written.
3. I would put a greater emphasis on the user interface. Given what we know about graphical user interfaces today, it wouldn't be hard to improve the interface dramatically. I would put the icons into a floating palette as in HyperCard, replacing the long menu area that takes up so much screen space. I would put the operations on icons into pull-down menus. I would get rid of the bottom four areas in the Pygmalion window entirely. The "mouse" area was necessary because the system was pretty modal; I would redesign it to be modeless. I would make greater use of overlapping windows (which hadn't been invented when this work was done). I would improve the graphics esthetics. With today's graphics resources--bit mapped screens, processor power, graphics editors, experienced bit map graphics artists--there is no longer any excuse for poor appearance. Good esthetics are an important factor in the users' enjoyment of a system, and enjoyment is crucial to creativity.
Intended users: Programmers
Types of examples: Multiple examples to demonstrate branches of a conditional, and recursion.
Program constructs: Variables, loops, conditionals, recursion
Table of Contents Watch What I Do