 Table of Contents
Table of Contents  Watch What I Do
Watch What I Do

This paper presents Tinker, a system that permits a beginning programmer to write Lisp programs by providing concrete examples of input data, and typing Lisp expressions or providing mouse input that directs the system how to handle each example. The user explicitly indicates which objects serve as examples, and may present multiple examples that serve to illustrate conditional procedures. The machine records the steps of the computation, and formulates a program to handle the general case.
Tinker provides some capabilities that remain unique among programming by demonstration systems. As a programmer's system, it requires more knowledge of a programming language than a purely direct-manipulation interface, but provides access to more computational power as a result. It is perhaps the most computationally general programming by demonstration system, capable of synthesizing any procedure expressible in its underlying Lisp language. It remains one of the few that accepts multiple examples, enabling conditionals and recursion. Each set of examples constitutes a partial definition, which can be incrementally augmented with positive or negative examples.
But people don't work that way. Teachers can never be absolutely sure that they are presenting rules that are correct and complete, nor can students ever be sure that they are learning all and only the correct principles. Concrete examples serve as a means for both students and teachers to check their understanding and reduce reliance on limited short-term memory. If the procedure to be learned is at all complex, examples should be demonstrated step-by-step, so that if an anomaly appears at any point, the teacher or student will know which step was at fault. Lawler [Lawler 85] relates a compelling case of the superiority of example-based learning. A child who was unable to reliably perform addition with numbers written on paper (where numbers were abstractions) was nevertheless quite competent in adding the value of coins when she needed to buy something!
Teaching is also a learning experience for the teacher. Teachers often remark that the process of teaching a subject leads to deepening their own understanding of that subject. "I thought I understood the material before, but after teaching it, now I feel I really understand it!" a teacher will often say. This understanding often develops in the process of elaborating examples for the benefit of students. Part of good teaching requires teachers to put themselves in the students' shoes to verify to themselves that each lesson is succeeding in conveying the intended information. Checking the connection between abstract knowledge and concrete examples helps the teacher to empathize with the students' viewpoint.
If examples play such an important role in teaching, the analogy between teaching and programming leads us to ask, Why can't examples play a more important role in programming?
Tinker is an experimental programming environment I have implemented to test the hypothesis that using examples in programming will yield the same kind of benefits as using examples in teaching. Tinker behaves like a (very dull) student, starting out by merely remembering the examples shown, and the steps that the teacher performs.
Since Tinker doesn't have a human student's capacity to automatically decide what features of one example may be relevant for future examples, the programmer must tell Tinker which features of the examples are important, and which can be ignored in general. Once this is done, though, Tinker can generalize a procedure from watching its operation in specific examples. Furthermore, like a good student, Tinker can build up its knowledge little by little. A sequence of examples can be shown, starting with simple examples illustrating common cases and leading up to complicated procedures for exceptional cases. At each step, Tinker always shows its teacher what it has learned so far, both in the effect of what it has been told on particular examples, and in the form of a Lisp program. The programmer can then correct any misconceptions on Tinker's part before proceeding to the next step, so that testing a program happens while the program is written, rather than afterward.
The kids had little difficulty learning about the turtle, a graphics cursor they could use to draw pictures using commands like Forward 100 and Right 90. Teachers would introduce Logo to students by having them type these commands to the computer and watch the responses of the turtle. Often, the biggest hurdle was that the children were very slow at typing on a keyboard.
The following sequence of turtle commands could draw a triangle.
Forward 100
Right 120
Forward 100
Right 120
Forward
100
Right 120
But trouble came when the teachers tried to introduce the notion of procedures. The simplest notion of a procedure is introducing a name for a group of turtle commands, using the Logo command To. To make a procedure that draws a Triangle, the student must say
To Triangle
Repeat 3 (Forward 100 Right 120)
End
But when the student types Forward 100 this time, the turtle doesn't move! Why not?! Was something wrong with the computer, the student wondered? The teacher then had to patiently explain that the computer was just remembering that it was supposed to do the Forward 100 as part of the Triangle procedure, and you couldn't actually get it to do anything until you finished the procedure (with End) and called it by typing Triangle. But this explanation seemed very abstract to a beginner, who was just trying to learn the concept of a procedure.
Furthermore, it seemed to require that you type everything twice! Once you performed the turtle commands that drew a triangle on the screen, why did you have to type those commands all over again just to have the computer remember them to make a Triangle procedure?
The teachers came up with a very ingenious solution to this. Around 1971, teacher Cynthia Solomon wrote Instant Turtle, an interface to Logo that introduced the notion of a procedure as a remembered set of turtle commands. Whenever the student typed a turtle command, it would always be remembered in a list. A new command, Teach, would take the current list of turtle commands, and make a procedure out of it, asking the student for a name. This new procedure was then available as another command. Teach in Instant Turtle was probably the first instance of a "macro recorder", now common in spreadsheets and word processing programs.
This turned out to be an enormous success. A student could issue the turtle commands for drawing a triangle, and get the immediate feedback of seeing the triangle appear on the screen. The student could then simply do Teach Triangle to make a triangle procedure, without retyping the Forward and Right commands.
This is a very simple kind of "programming by demonstration", since the triangle drawn on the screen serves as an example of what the Triangle procedure will do. Even if the procedure did not have arguments, a triangle drawn the next time the procedure was called still might be different, appearing at a different place on the screen or in a different orientation. Showing the computer how to draw an example triangle could be used to teach the machine how to draw triangles in general, just as showing a person an example of how to perform a procedure can help them learn that procedure.
But Instant Turtle was very limited in its expressive power, and as soon as a child gained mastery of basic turtle manipulation and the concept of a procedure, it was time to move on to full Logo. After all, Instant Turtle couldn't define procedures with input arguments, procedures that called other Logo procedures or that called themselves recursively, or procedures that contained conditionals. But moving from Instant Turtle to full Logo loses the immediacy of defining procedures from remembered sets of interactively executed actions. Is it possible to create a programming environment as friendly as Instant Turtle, but for a language as powerful as Lisp? Could procedures be defined by demonstrating them on concrete examples, always giving the user immediate feedback, without sacrificing expressive power? This is the motivation that led to my work on Tinker.

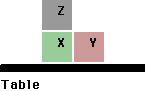
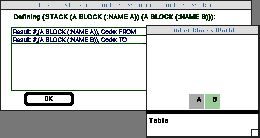
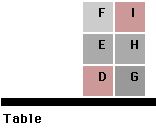
This problem is demonstrated using multiple examples. First, we start out with a simple example that defines the base case, then give a more complicated example. The first two cases are illustrated below. In Figure 1, the task is to put Block A on Block B, in Figure 2, to put Block X on Block Y. More examples can be shown later.
If we don't want a remembered procedure to do the same thing every time it is called, it must have some way to make a decision among alternative courses of action. To demonstrate this to Tinker, we must show several examples for the same procedure, each illustrating what happens in case each of the alternatives is chosen.
If a teacher shows a student several examples for the same concept that receive different treatment, the bright student will raise his or her hand and ask the teacher "How did you decide which alternative to use?". The teacher is being asked to provide decision criteria by which a new example could be classified as being like one of the alternative examples already presented. The teacher who is trying to teach a procedure involving decision making should show students at least one example in which the decision turns out to be each of the possible alternatives. This is analogous to the programmer's truism that a program containing a conditional must be tested with at least one example for each of the conditional branches. When more than one example is provided for a function, Tinker acts like that bright student. For each new example, it asks the user to provide a test which can distinguish the most recent example from others it already knows.

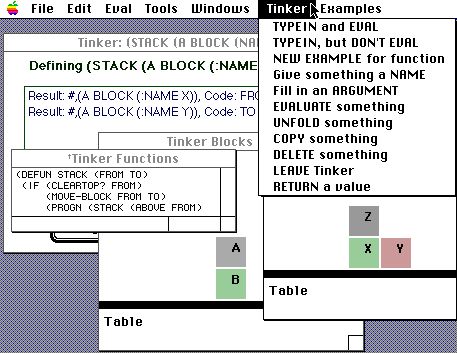
The first two operations on Tinker's menu (see Figure 3), TYPEIN and EVAL/Don't EVAL allow the user to introduce new Lisp expressions into Tinker's Snapshot Window. The third operation designates an existing expression as a new example for a function. The remaining operations edit expressions in the snapshot window, and finally the last operation, RETURN, signals the end of a function definition.
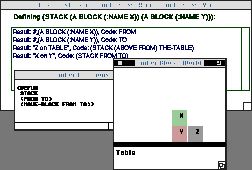
To start defining the Stack function, we imagine that such a function had already been defined, and show Tinker how we would call it in our example. We set up the blocks world illustrated in Figure 4, and call Stack on two arguments, Block-A and Block-B. We assign the name From to Block-A and the name To to Block-B. These are the arguments to the Stack function. Thus, Block-A becomes an example of a From block, and Block-B is an example of a To block.
Instant
Turtle and its kin are only suitable for imperative domains like graphics,
where each command is performed for its side effect. In functional languages
like Lisp and Logo, expressions return values, and a value returned by one
expression can be used as an argument to another function. How does this
concept fit into a programming by demonstration system?
In Tinker, when an item is selected as an argument to a function, the value of its result part is used, but the code part gets carried along as a component of the code part for the function call. The result part appears before the code part in each entry to emphasize that it is the value of the result that will be used when the entry is selected as an argument to another function. Thus, Tinker records the complete history of dependencies between Lisp values and the code that produced them.
The idea of a procedure as a remembered set of actions is generalized in Tinker from a simple linear list as in Instant Turtle and simple keyboard macros, to the tree structure necessary for building expressions in a functional language. The key idea is that the result, or value, produced by a set of actions can be used as input to subsequent actions.
Beginners typically have difficulty programming complex expressions involving nested function calls. They find it hard to keep in their heads what the effect of each subexpression will be. Tinker relieves this problem by allowing a beginning programmer to build up a complicated expression incrementally, examining the result of each piece in a representative case before using it as part of some larger expression.
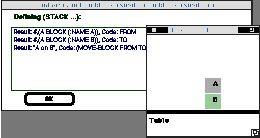
However, the code that Tinker remembers for this operation is not
(Move-Block Block-A Block-B), but instead
(Move-Block From
To)
Since Block-A and Block-B only serve as examples of From and To blocks, Tinker generalizes the code so that future invocations of Stack will perform the operation on whatever objects take the place of Block-A and Block-B.
Figure 5: After performing the Move-Block operation
The
result of this is a somewhat trivial definition of the Stack function that
simply calls Move-Block. Next we show it the more complicated example involving
Blocks X, Y, and Z. In this case, moving the From block to the To block will
not work. We must teach Tinker how to remove obstacles.
We must take care to teach Tinker how to remove the obstacle in such a way that the system can make appropriate generalizations. If we were to simply do the concrete operations,
(Move-Block Block-Z The-Table) and
(Move-Block Block-X
Block-Y),
Tinker would not learn the relationship between Block-Z and Block-X, although it would indeed appear to accomplish the task in this specific example. The procedure would not then work correctly in future examples.
Figure 6. Preparing to teach Tinker about obstacles. The goal is to stack X on Y, but Z is in the way.
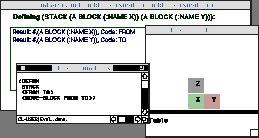
First, we have to show Tinker what is special about Block-Z. Every block responds to the function Above, which either returns the block Above it, or NIL if none exists. We type the function Above, then select the line in the Snapshot Window that shows Block-X as the From block. Tinker then displays:
Result: #,(A 'block :name 'Z), Code: (Above From)
This shows Tinker that we chose Block-Z by virtue of its standing in the Above relation to the From block, e.g. Block-X.
Alternatively, the teacher can start with a complex example, and show how it can be reduced to simpler examples, then simpler ones still, until finally a trivial example has a trivial solution. This is a top down style. Finally, in either style, a test for recognizing the base case must be presented, to show how to determine when to stop the recursion.
Tinker supports both the top down and bottom up methods of building recursive functions from examples. A bottom up style starts with defining an "incorrect" procedure that handles the base case only. An example for the recursive case makes use of the already defined base case procedure, and having two examples leads to constructing a test that distinguishes them. Starting with the recursive case, computation "whittles down" the procedure to simpler cases. When the base case is reached, the New example operation can be invoked from within the definition of the non-trivial case.
In the Stack example, we would now like to call the Stack function recursively on the obstacle block and the object The-Table. This creates a possibly ambiguous situation: are we making reference to the definition of Stack that we previously completed (a bottom-up style) or the one that is underway now (a top-down style)? Tinker's approach to this subtle problem is to enlist the user's help by asking which previous example is the "closest" to the present case. The following question is posed.
Which example is (Stack Block-Z The-Table) most similar
to?
(Stack Block-A Block-B)
(Stack Block-X Block-Y)
We reply that it is similar to the first case. Now, Tinker removes the obstacle Block-Z and places it on the table.
Figure 7. The obstacle is removed
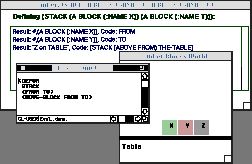
We
complete the definition by moving the unobstructed Block-X to the To block,
Block-Y.
Tinker
displays two Snapshot Windows, each displaying one of the cases, and asks the
user to define an expression that will separate the cases (See Figure 9). Each
evaluation step is displayed simultaneously in both windows. For the condition
to be valid as a decision rule, it is constrained to evaluate to true in
one of the cases and false in the other case.
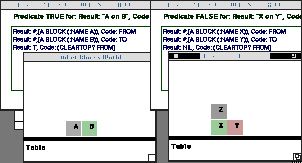
The
predicate expression calls the function Cleartop? which asks a block
if its Above block is NIL. Cleartop? is true when applied to Block-A
and false when asked of Block-X.
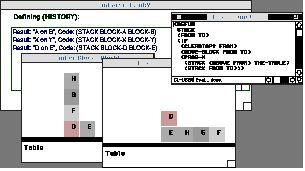
Tinker creates a recursive definition, incorporating a conditional expression, as shown in the window containing the Lisp definition at the upper right of Figure 10.
To test it, we give it a configuration of blocks containing several obstacles on the From block, and Stack is called recursively several times in order to get rid of all the obstacles, before performing the Move-Block operation. Similarly, we can show Tinker another example (Figure 11), building a stack of Block 1 on Block 2, that demonstrates how to clear obstacles on the To block instead of on the From block. Then, Tinker will be capable of doing by itself a more ambitious example (Figure 12), a stack with Block D on Block G, that contains obstacles on both the From and To blocks.
To learn from an example, it is necessary to know which features of the example are important. When an example is presented to Tinker, the programmer indicates which constants in the example are to be generalized when Tinker constructs a function definition. Although Tinker lacks the capability of automatically figuring out what is important in an example the way a human student would, keeping a close correspondence between a concrete example and a general procedure ensures that the programmer's intentions are faithfully captured.
Examples that show the similarities and differences between one idea and related ideas help clarify principles. Tinker constructs conditionals by presenting one example for each important case in the resulting program. Because conditional procedures are developed in this way, no untested code can arise in the final program.
A sequence of examples should start with simple examples and build to more complex examples and exceptional cases. Recursive and conditional procedures can be developed incrementally by starting with simple, "incorrect" definitions, and later adding more examples to handle more complicated and special purpose situations. As we have indicated, it is also possible to go in the other direction, but some care must be taken to inform the student that more information is forthcoming.
I hope that the examples of programming in Tinker shown above illustrate how Tinker gives students practice in the art of example selection by rewarding appropriate choices of examples. Since examples play such a crucial role in teaching and learning, an example based programming environment such as Tinker should be a superior vehicle for learning programming.
Intended users: Beginning programmers
Types of examples: Uses multiple examples to define conditionals and recursive programs.
Program constructs: Variables, conditionals, recursion
 Table of Contents
Table of Contents  Watch What I Do
Watch What I Do