back to ...

Chapter
3 A Predictive Calculator

Ian H. Witten

Introduction

One way of giving casual users access to some of the power of a computer without having to learn formal programming methods is to enable tasks to be defined by giving examples of their execution, rather than by a procedural specification. This chapter summarizes a 1981 proposal for an electronic calculator that allows iterative computations to be inferred interactively from an initial part of the sequence of key-presses [Witten 81]. The aim was to construct a device that is partially self-programming. The predictive calculator was implemented on a PDP-11/40 computer in 1981. It was intended as a demonstration rather than a practical tool for casual users, and the user interface was not completely polished.

The idea of defining problems operationally through examples was proposed in the "query-by-example" system for database retrieval [Zloof 77b], which was intended for a user with no programming and little mathematical experience. To specify what to retrieve, you present an example of an item that should be included. The scheme illustrates that useful interactive systems can be built that allow users to define non-trivial tasks by example. One of its advantages is that it frees users from thinking of the retrieval problem in an artificially sequential form: instead they can specify the links, conditions, and constraints in any order. In contrast, the present work explores how strictly sequential information can be inferred by a machine from an initial subsequence.

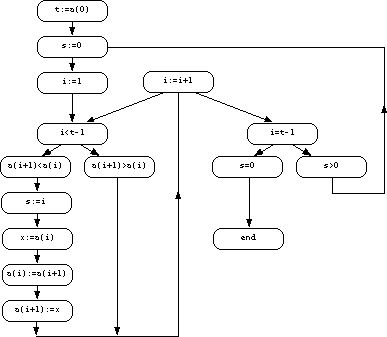
Figure 1. Trace of a sorting process

Automatic inference of programs from traces is another domain in which the problem is specified by an example. When a detailed trace of a particular execution of a program is available at the right level of generality, program inference can be easy. For instance, [Biermann 72] discusses the inference of Turing machines from traces of sample computations. The problem is more usefully addressed at a higher level than Turing-machine instructions, and [Gaines 76] gave the programming-language-level trace in Figure 1 as an example of a sorting program that performs a simple bubble-sort. The flowchart in Figure 2 can be derived from the trace simply by assigning different states to different statements and drawing sequential links between them. It is correct and complete except for a link from the assignment "i:=1" to the test "i=t-1" which was not demonstrated by that particular example. However, it is unlikely that such a trace would be entered without error, and even if it were, it may not be any easier for a casual user to generate than a structural description--a program--for the sorting process. Traces can be useful, though, in more limited domains--as this chapter will show.

Figure 2. Program formed from the trace

Programming a Calculator by Demonstration

When using interactive computers, there are many situations in which it is hard to decide whether to do a minor, but repetitive, task by hand or write a program to accomplish it. Simple, repetitive arithmetic calculations often present this quandary. For example, to plot y = xe^1-x for a dozen or so values of x, should one use a hand calculator or write a BASIC program? The first is easier and more certain; it will not take more than 10 minutes. The second may be quicker, but could require consulting the manual to refresh one's memory of the vagaries of BASIC syntax.

The Predictive Calculator is a system that quietly "looks over the shoulder" of the user, forming a model of the action sequence. After a while it may be able to predict what keys will be pressed next. Any that cannot be predicted correspond to "input." Thus the system can eventually behave exactly as though it had been explicitly programmed for the task, waiting for the user to enter a number and simulating the appropriate sequence of key-presses to calculate the answer. The user must pay a price for the service, for the system cannot help but be wrong occasionally; moreover, extra keys must be provided to enable predictions to be accepted or rejected.

Sample dialogues

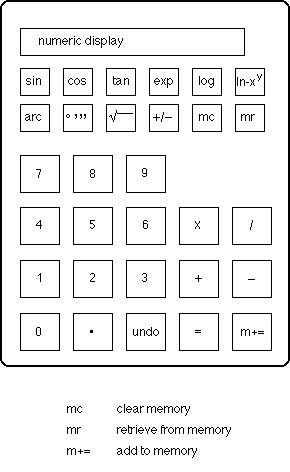
The device is based on the simple, non-programmable pocket calculator shown at the beginning of this chapter. An adaptive model is constructed of the sequence of keys that are pressed. If the task is repetitive (like computing a simple function for various argument values), the system will soon catch on to the sequence and begin to activate the keys itself. When the prediction is wrong an undo key was envisaged to enable the user to correct it by undoing a single step of the sequence (though, as noted above, the interface was never completely finished). In order to keep control in the hands of the user, predictions are indicated but not actually made until they have been confirmed by an accept key. One can imagine being able to switch into a "free-run" mode after having gained enough confidence in the predictions, but this was not implemented.

Figures 3-5 give examples of this "self-programming" calculator. The first shows the evaluation of xe^1-x for a range of values of x. The keys pressed by the operator are in normal type; those predicted by the system are shaded. From halfway through the second iteration onwards, the device behaves as though it had been explicitly programmed for the job (except for the need to repeatedly press accept or switch into free-run mode). It waits for the user to enter a number, and displays the answer. It takes slightly longer for the constant 1 to be predicted than the preceding operators because the system requires an additional confirmation before venturing to predict a number (see below). Provided the user enters variable data before any fixed constants (and people generally do this), there is no difficulty in getting the calculator to pause when the answer has been reached: it stops automatically whenever it cannot predict the next element in a sequence and this occurs at the end of each of the four calculations in Figure 3.

Figure 4 shows the evaluation of

1 + F(log x,8 log 2)

for various values of x. The first line stores the constant log 2 in memory.

More complicated is the evaluation of

20 + 10 log BBC[(1 + a² - 2a cos F(180x,4000)) - 10 log [1 + a² - 2a cos 45]

for a=0.9, shown in Figure 5. Since the calculator possesses only one memory location, it is expedient to compute the last sub-expression first and jot down the result. The result of this calculation (-2.69858) only has to be keyed twice before the system picks it up as predictable. Some interference occurs between this initial task and the main repeated calculation, and three suggestions had to be "undone" by the user.

If an erroneous suggestion is made, indicated by an "undo," the system is cautious about making a prediction in that context in the future. Any step that is undone is erased from the system's model of the interaction, leaving no record of its existence. Of course, the user will (presumably) have followed the undo by an action that is different from the one predicted, creating a conflict in the model. Consequently when the same context occurs again, no prediction will be offered to the user. However, the system will internally monitor its own predictions in that context, and when several correct predictions have been made subsequently (but not presented to the user), it will eventually venture its suggestions. This is the reason why the penultimate "+" on each line of Figure 5 has to be keyed by the user several times. Both of the sequences

log x 10 =

log x 10 +

had occurred in the interaction, but a long run of the second was enough to cause it to be used eventually.

As Figure 5 implies, any number that appears in the input sequence is identified and treated as a single unit. To enable the predictions that follow numbers to be made in time for them to be useful, it was necessary to provide a special key with which each number is terminated. Of course, operations like "cos", although written as three letters in the figure, already correspond to a single keystroke and so no terminator is needed.

The modeling technique

The system uses an extremely simple method to form its predictions. The user's input sequence is characterized by the set of overlapping k-tuples of symbols that occur in it, for some limited context length k (k=4 in the examples of Figures 3-5). The symbols are either numbers or operation keys. For instance, Figure 6 shows the 4-tuples that are stored for the sequence of Figure 3.

.1 mc m+= +/- mc m+= +/- + m+= +/- + 1 +/- + 1 = + 1 = exp * * *xmr = .2 mr = .2 mc = .2 mc m+= .2 mc m+= +/- * * *

Figure 6. The basic model that is stored for the sequence of Figure 3

The first row shows the first four symbols in the sequence, the second shows the 4-tuple starting at the second symbol, the third starts at the third symbol, and so on. To use these for prediction, whenever the last k-1 symbols entered match those that begin a stored tuple, the last symbol of that tuple is predicted. For instance, if the user enters "m+= +/- +" this matches the third row, so the system will predict 1.

This modeling technique, known as a "length-k" modeling [Witten 79], arose out of context modeling techniques [Andreae 77]. It turns out that the k-tuples can be stored economically by massaging them into the form of an automaton model, although this is hardly necessary with modern store sizes. A more powerful, though slightly less space-efficient, prediction technique is to use partial matching on the k-tuples in conjunction with a trie-structured model (e.g. the REACTIVE KEYBOARD [Darragh 92] and the PPM text compression method [Bell 90]); that would be the natural way to implement the predictive calculator nowadays. What is surprising is that the simplistic modeling technique that was actually implemented performed so well in practice.

A modification to the modeling technique was made to suit the calculator situation. It is clear from a cursory analysis of calculator sequences that numbers and operators should be treated differently, for a typical sequence comprises different numbers embedded in a fixed template of operators. This rule is not universal, because fixed constants appear in the stream as well as variable input data. Note how the constants 1 in Figure 3, 8 and 1 in Figure 4, and 4000, 180, 2, .9, 1, 10, 20 and 2.69858 in Figure 5 are all quickly picked out as predictable by the system.

In order to prevent differences in data values from rendering the length-k sequences inoperative, two parallel sets of k-tuples were used. One was exactly as shown above, whereas the other mapped all input numbers into the same token <NUM>, yielding Figure 7 from Figure 6.

Predictions from this model were only used when the other one failed to yield a prediction. For example, when the first prediction of Figure 3 is made, the "+/-" on the second line, it is predicted from the tuple "<NUM> mc m+= +/-", because the actual context ".2 mc m+=" has not been seen before. Furthermore, the system was constructed to be more conservative about predicting numbers than operators. No prediction was made unless it would have been correct the previous n times it occurred, and n was set differently for operators (n=1) and numbers (n=2). Thus the tuple "m+= +/- + 1" is not used to predict the 1 on the second line of Figure 3, but it is used on the third line.

<NUM> mc m+= +/- mc m+= +/- + m+= +/- + <NUM> +/- + <NUM> = + <NUM> = exp * * *xmr = <NUM> mr = <NUM> mc = <NUM> mc m+= <NUM> mc m+= +/- * * *

Figure 7. The mapped model that is constructed from Figure 6

Except for its ability to parse numbers in the symbol string and to distinguish numbers from operators, the system incorporates no knowledge about the calculator or calculation sequences. For example, it will learn nonsense sequences like "1 1 + + 1 1 + +" and regurgitate them just as readily as syntactically meaningful sequences. (The sequence "x x" that occurs in Figure 5 may seem anomalous; in fact it is the calculator's way of squaring a number.) The procedure is entirely lexical and does not recognize patterns of numbers. For example, in the sequence .1, .2, .3, ... of Figure 3 it is evident what should come next but the system does not spot the pattern. Also, it does not notice multiple occurrences of the same input data. For example, if x exp(1-x) were to be evaluated on a calculator without a memory, x would have to be entered twice. The modeling procedure is incapable of exploiting this redundancy.

A common source of variation in calculator sequences is the discovery of an easier way to do the task. For example, halfway through Figure 5 one may decide to enter 1.81 directly instead of ".9 x x = + 1". This is unlikely in the present example, for no penalty is associated with the latter sequence once it has been learned. However, if the simplifying discovery is made early on in the interaction it may cause some incorrect predictions.

Conclusion

This system illustrates how systematic processing of a "history list" of previous interactions can be used to predict future entries. Rather than being invoked explicitly, the history list is accessed implicitly to provide assistance to the user.

Despite the fact that the modeler has no knowledge of the syntax or semantics of the dialogue, it is remarkably successful. For example, when the three short repetitive problems of Figure 3-5 were concatenated into a single input sequence, over 75% of the sequence elements were predicted and less than 1.5% of predictions were incorrect. There is always a temptation to adjust system parameters in retrospect to yield good performance, and when this was done, nearly 80% of correct predictions were achieved with an error rate of under 0.5%.

The basic idea behind the predictive calculator has been engineered into a device called the REACTIVE KEYBOARD that accelerates typewritten communication with a computer system by predicting what the user is going to type next [Darragh 92]. Obviously, as with the calculator, predictions are not always correct, but they are correct often enough to form the basis of a useful communication device. Since predictions are created adaptively, based on what the user has already typed in this session or in previous ones, the system conforms to whatever kind of text is being entered. It has proven extremely useful for people with certain kinds of communication disability.

Acknowledgments

It is a great pleasure to acknowledge the influence and encouragement of Brian Gaines, John Cleary, and especially John Andreae. John Darragh skillfully implemented the predictive calculator program on a PDP-11/40 computer.

Predictive Calculator

Uses and Users

Application domain: Calculator

User Interaction

How does the user create, execute and modify programs?
User creates programs simply by using the calculator. There is no special learning mode. The only user interaction, beyond doing the task, is to press Undo when the predictor makes a mistake.
By rejecting a prediction, the user forces the calculator to learn a new prediction from that context.

Inference

Inferencing:
Keeps a history of all four-token sequences (a token is a number or an operator). Whenever the user types three tokens that match a recorded sequence, the Predictive Calculator predicts the fourth. (Any fixed value can be used instead of "four").

Program constructs:
Can ask for user input for any data that varies, but cannot create a variable (e.g. it does not identify the two X's in "X² + 5X")

Knowledge

Types and sources of information:
No syntactic rules. (e.g. it will happily learn the sequence "1 1 + + 1 1 + + " if that is what the user enters)

Implementation

Machine, language, size, date: PDP-11/40, 1982.