
 Table of Contents
Table of Contents  Watch What I Do
Watch What I Do
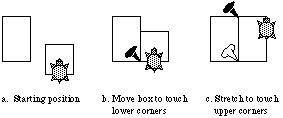
Metamouse helps users express their intent through a "teaching" metaphor. Users teach a graphical turtle named Basil. (Throughout this chapter "Basil" refers to the agent perceived by the user and "Metamouse" to the underlying system.) To teach effectively, users must appreciate Basil's limited powers of perception and inference. A brief "biography" (shown in Figure 1) introduces new users to the way Basil learns about spatial relations in terms of touch (the basis of graphical construction). In use, the system shows its focus by moving the turtle to the location of each edit, highlighting the things it senses.
The teaching metaphor motivates the use of an agent, incremental learning, and feedback situated on the data. The agent Basil conveys a task model based on graphical construction, with an appropriate focus of attention and rules of inference. Users come to understand that since Basil works by touch, they must express measurements normally done "by eye" as graphical constructions. The system learns incrementally, and enforces incremental teaching by displaying constraints and predicting actions. Basil moves among the user's data and situates its messages or queries about constraints on the objects concerned.
This chapter describes Metamouse's design, implementation and evaluation. The design decisions flesh out an "instructible agent" approach to programming by demonstration. The implementation shows that such a system is possible and capable of real-time response, although the mechanisms we chose are complicated. An evaluation by a group of users reveals some important limitations that make teaching Basil needlessly difficult.

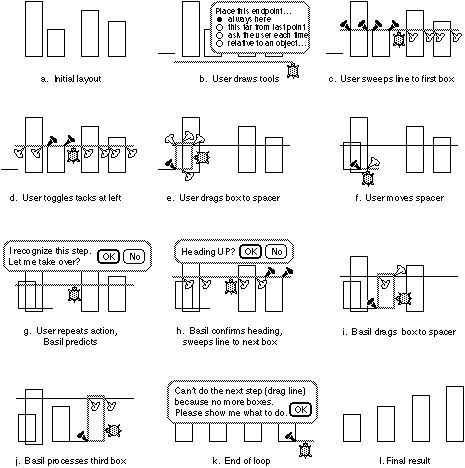
(Note that the scenario outlined above is a bit fanciful: Metamouse is only an experimental system residing in a very simple editor for boxes and lines.) Figure 2 shows a trace of Pam teaching Basil to sort boxes.
As a first step, Pam draws a short line at the left of the screen, a spacer she will use to set the distance between boxes (Figure 2b). Its endpoints touch nothing, so Basil infers that their location is set by the user (i.e. they are inputs). Pam draws another line below the boxes: she will sweep this upward to the top of each box in turn, to select them in order by height. As with the spacer, Basil infers that the endpoints are inputs, but Pam replies through the dialog box (2b) that she wants Basil to draw this line always at the same place. She then picks it and drags it up to the first box-top in its path (2c).
Basil highlights points where the sweepline touches each box. Black tacks mark significant touches, where the line meets a vertex or midpoint of an edge. Metamouse's inference rules rate all such contacts as equally constraining. White tacks indicate unimportant contacts, as rated by the inference rules. It so happens that a neighboring box is just twice the height of the shortest one, so Basil has put black tacks on its left and right sides. Pam understands that she can override these inferences by clicking on the tacks, changing them to white (2d).
Having picked the shortest box, Pam moves it to the spacer (2e). Although both box and spacer touch other objects as well, Basil puts a black tack only where they meet, so Pam knows it views this as the one important constraint. Finally, she advances the spacer to the opposite side (2f).
When Pam picks the sweepline a second time, Basil detects repetition and predicts a loop, offering to do the next step (2g). She assents; Basil confirms the direction of search (2h) and sweeps the line up to the next shortest box. Basil picks this box, rather than return to the first one or choose one at random, because it inferred three things from the first example: that it should choose a box not encountered before; that it should scan upwards; and that it should pick the first one in its path.
Asking Pam to approve each step before continuing, Basil performs all editing (2i,j) until no boxes remains above the sweepline. The failure to find another box terminates the loop (2k). Basil then asks Pam to demonstrate the rest of the task. She removes the construction tools and signals that the lesson is over.
Later, when Pam invokes this program again from the tasks menu, Basil will create a sweepline and spacer as before, inviting the user to edit the spacer, since its endpoints are inputs. Then it will do the entire sort, regardless of the number of boxes. It will sort correctly, provided the boxes are initially aligned at the bottom so the sweepline does indeed select them in order by height.
Inducing transformations directly from examples of input and output is a completely intractable problem [Angluin 83]. The effect of a demonstration is to decompose the transformation into a sequence of simpler ones. Although drawing is inherently procedural [van Sommers 84], it is not easy to induce procedures from demonstrations because typical users do not always construct the relevant measurements and relations but work instead by visual inspection. Moreover, examining the whole screen for implicit spatial relations would require an infeasible number of tests, and vastly expand the space of hypotheses.
To cope with these difficulties, Metamouse focuses attention on visible touch relations caused by actions, requiring users to specify complex relations by constructing them. To help users understand this approach we adopted a teaching metaphor that combines demonstration, questions, prediction, correction and direct instruction. Our hypothesis was that by teaching Basil, the user would gain insights needed to use appropriate constructions. The metaphor encourages the user to take an intentional stance toward the system [Dennett 87], rather than try to understand its inference mechanisms.
Rules of interaction between human teachers and pupils have been formulated as "felicity conditions" [van Lehn 83]. We adapted four of them to teaching Basil: correctness (examples shown are assumed to be correct), show work (demonstrate execution rather than just input and output), no invisible objects (express constraints by graphical construction), and focus activity (eliminate extraneous actions). To help untrained teachers obey "show work" and "no invisible objects," Basil reminds them that it is short-sighted and asks them to draw constructions when it finds no touch constraints. To help users obey "correctness" and "focus activity," Basil eagerly predicts actions as soon as it detects repetition, which gives the user an early opportunity to validate what it has learned, and also minimizes the chance of the user confusing Basil by accidentally varying the way actions are done.
The Metamouse system contains elements of both similarity- and explanation-based learning (see [Witten 88]), for an account of the distinction). Similarity-based learning is used to find loops and branches. Positive examples are user demonstrations. Negative examples are predictions that the user rejects. Flow of control is represented by production rules whose context (left-hand side) is a sequence of actions and whose prediction (right-hand) is the next action. Rules are maximally general, having the shortest context that nonetheless predicts deterministically. Negative examples cause the system to form new rules and specialize old ones by lengthening their context. Positive examples have the effect of "reinforcing" a generalized rule by adding to the set of cases that any specialization would have to cover.
Explanation-based learning is used in two ways. First, the user is encouraged to "explain" a task by employing constructive techniques to reveal implicit relationships. This differs from conventional explanation-based learning in that the user is responsible for the explanation. Second, to identify touch constraints Metamouse applies a simple theory that distinguishes levels of significance in observed touches. This is a classic use of explanation-based learning to choose, via domain theory, a subset of the information available in a single example that serves to identify an equivalent situation in the future.
The Tasks menu contains names of procedures the user has taught Basil. The user may select from this while teaching, to embed tasks, although such "subroutines" inherit no variables (parameters) from the current procedure.
The turtle icon has three functions. First, it reminds users that they are teaching. Second, it indicates Metamouse's focus of attention: Basil's snout touches the coordinates of the most recent drawing action. Third, it lets the user set Basil's direction when searching: each click on the shell rotates it by 90deg..
Tacks mark observed touch relations (see Figure 2). Black tacks mark important constraints; white ones mark incidental touches. If the user disagrees, she may click on a tack to change its color, thereby overriding Basil's inference.
Dialog boxes present the system's hypotheses about a direction of search or implicit constraints (see Figure 2).
There are several display options, intended mainly for use in our research. The turtle icon may be shown at all times during a lesson, or only when Basil is predicting an action, or not at all. Tacks of either color may be shown or hidden.
operator: drag
grasping: line-01.midpoint * the thing dragged, i.e.
the Sweepline
postconditions:
position (145, 93) * (x,y)
location of grasp point, i.e. Basil's snout
distance (145, 11) *
change in x and y coordinates
heading (0x, +y) * approx. relative
motion in x and y directions
touch (line-01.? : box-17.left.midpt)
* leftmost box in Figure 2c
touch (line-01.? :
box-17.right.midpt)
touch (line-01.? : box-42.top.left) * the box the
user wants
touch (line-01.? : box-42.top.right)
touch (line-01.? :
box-11.left.?) * third from left in Figure 2c
touch (line-01.? :
box-11.right.?)
touch (line-01.? : box-91.left.?) * rightmost in
Figure 2c
touch (line-01.? : box-91.right.?)
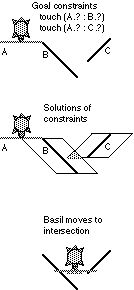
Touch relations specify parts of objects in contact. A question mark `?' indicates that the contact may occur anywhere along an edge (Metamouse also records the specific location, not shown); a part like "top.left" indicates a vertex. Line-01 (the Sweepline) touches the top of box-42 and the sides of the other three boxes.
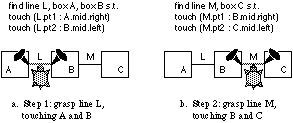
Figure 3. Teaching Basil to find a chain of boxes, in two steps. The user selects different parts of it so that Basil observes all the touches that link the boxes.
Metamouse
does not record spatial relations like alignment or distance between objects,
nor touch relations between objects other than the currently selected one.
Headings are approximated: 0x means > 45deg. off the x axis, +y means <=
45deg. off the positive y. Recording only part of the state constitutes
implicit generalization, which biases what Metamouse can learn and the way it
must be taught. For instance, if the user wants Metamouse to learn a structure
made of several objects, she must walk Basil across it, as illustrated in
Figure 3.
Metamouse checks each object referred to by the current action, to see whether it occurred in a previous step. If so, Metamouse copies the variable from that step into the current one and sets the selector to leave the value unchanged. Otherwise, Metamouse makes a new variable, whose selector is find or create, depending on whether the action selected an existing object or drew a new one. With variables, the action in Figure 2c now reads (changes highlighted in bold):
operator: drag
grasping: Sweepline.midpoint
postconditions:
position (145, 93)
distance (145, 11)
heading (0x, +y)
touch
(Sweepline.? : Box1.left.midpt)
touch (Sweepline.? :
Box1.right.midpt)
touch (Sweepline.? :
Box2.top.left)
touch (Sweepline.? :
Box2.top.right)
touch (Sweepline.? : Box3.left.?)
touch (Sweepline.? : Box3.right.?)
touch (Sweepline.?
: Box4.left.?)
touch (Sweepline.? : Box4.right.?)
where
Sweepline := current value [line-01] * value
unchanged
* history of values is
[line-01]
Box1 := find box [box-17] * selector "find box"
returns box-17
Box2 := find box [box-42] and pushes it onto
the history stack
Box3 := find box [box-11]
Box4 := find box
[box-91]
Variables may be thought of as representing roles [Rich 88] or data descriptions (see Chapter 5), such as "Sweepline: the object Basil grasped in the previous step," or "Box2: a box lying above Basil's previous position and not touched in this way during a previous iteration of this action." Metamouse has no way of telling the user about the role of an object, however.
action: DragToBoxTop
operator: drag
grasping:
Sweepline.midpoint
postconditions:
position (145, 93)
distance (145, 11)
constraint heading (0x, +y)
constraint touch
(Sweepline .? : Box1.left.midpt)
constraint touch (Sweepline .? :
Box1.right.midpt)
constraint touch (Sweepline.? : Box2.top.left)
constraint touch (Sweepline.? : Box2.top.right)
touch (Sweepline .? :
Box3.left.?)
touch (Sweepline .? : Box3.right.?)
touch (Sweepline .? :
Box4.left.?)
touch (Sweepline .? : Box4.right.?)
where
required Sweepline := current value [line-01]
required Box1 :=
find box [box-17]
required Box2 := find box [box-42]
Box3
:= find box [box-11]
Box4 := find box [box-91]
The rules assign each touch to one of eight levels of significance. The highest level, "determining," specifies particular objects and points of contact, thus exactly determining where Basil should move (no touches like this occur in the action above, but the contact between the box and the spacer in Figure 3d is determining). Lower levels represent increasing degrees of freedom in the choice of coordinates, as when moving a line so that any part of it crosses some vertex: the constraints above are of this type. The lowest level, "trivial," hold by definition.
The rules examine several aspects of a touch: first, whether it resulted from the action or remained in effect throughout (all the touches above resulted from the drag); second, the degrees of freedom implied by the types of parts involved (a vertex-vertex touch has 0 degrees, a vertex-edge has 1 (as in the example), an edge-edge has 2); and third, whether the objects are predetermined or not (i.e. variables are unchanged, rather than set by a find selector as in the example).
In the above, four touches get the same rating, so all are deemed constraints. Their variables are labeled "required", because Metamouse must keep them up to date when it does this action in future. It will ignore the other touches and variables. If some required variable (e.g. Box2) has a "find" selector, then heading is a constraint. If no touches rate above the "trivial" level, or no constraints are accepted by the user, then absolute position is inferred as the only constraint. In Figure 2d, Pam accepts the constraints involving box-42 but rejects touches with box-17, so they and variable Box1 will be ignored.
An incidental touch may introduce an object that turns out to be required for a constraint in some later step. When this happens, Metamouse reclassifies the touch as a constraint, on the assumption that its earlier appearance was no accident. (A weakness of the current system is that it does not notify the user of this change, which may override a decision the user made.)
Metamouse stores a history trace of all actions, as well as a list of the classes of actions learned and a set of production rules for predicting actions. When Pam drags the sweepline to the first box, Metamouse has already learned three action classes (mnemonic names made up for this exposition):
ActionClasses = {DrawSweepline, DrawSpacer, GraspSweepline}
The system compares the new action, DragToBoxTop, with each one. They must match exactly, but only operators, constraints and required variables are checked (cf. knowledge-intensive similarity-based generalization [Porter 90]). Operators must be identical. Headings match if at least one (x,y) component matches and the other one matches, is 0 or don't care; headings are the one feature Metamouse generalizes over multiple examples. Positions match if they lie within a small tolerance. Touch constraints match if object variables and part names match. Re-used variables match if they are identical; other variables match if they have the same selector. For speed, Metamouse checks operators first; in our example, none of the three previous actions is a "drag," so DragToBoxTop is immediately added to the list as a new class.
Metamouse does not do partial matching (which implies generalizing classes over multiple examples). We tested this idea in a pilot project but found that partial matching heuristics lead to over generalization and consequent false predictions unless additional information such as procedural context (i.e. preceding and following actions) is considered. Another strategy, in which raw, ungeneralized actions are matched with generalized classes, surprisingly proved unsatisfactory when we tested it. The match did not consider the "significance rating" of touches in the new action (since determining this would amount to generalizing) and as a result accepted many inappropriate matches. Figure 4 shows what can happen under this approach. The actions in frames b and c have a common touch (at the lower corners) which is significant in b but irrelevant in c; without testing for significance, however, touches in c would match all constraints in b.
Figure 4. Less rigorous matching strategies could permit actions b and c to match. The relevant touch in b (black tack) occurs in c (white tack), so in that sense c has all features required to match b. But the touches play different roles in each action, so they should not be matched.
R0 BeginTask -> DrawSweepline * not shown
R1 DrawSweepline ->
DrawSpacer * see Figure 2b
R3 DrawSpacer -> SelectSweepline *
not shown
R4 SelectSweepline -> UserDemosNewAction * 2c
Since DragToBoxTop matches no existing action class, it replaces UserDemos-NewAction in rule R4. The rest of the first iteration steps are given below.
R4 SelectSweepline -> DragToBoxTop * see Figure 2c
R5
DragToBoxTop -> SelectBox * not shown
R6 SelectBox -> DragBox
* 2e
R7 DragBox -> SelectSpacer * not shown
R8
SelectSpacer -> DragSpacer * 2f
R9 DragSpacer ->
UserDemosNewAction * 2g
When Pam grasps the sweepline a second time (see Figure 2g), this new action matches SelectSweepline, so Metamouse changes rule R9 to:
R9 DragSpacer -> SelectSweepline
Basil predicts the next action, DragToBoxTop, because the end of the trace now matches the left-hand side of rule R4. Basil continues predicting (another three iterations of rules R4 through R9) until R4 fails to fire because no boxes remain on which to instantiate its constraints. Pam then demonstrates deleting the sweepline and spacer. The final changes to the ruleset are:
R10 DragToBoxTop fails -> DeleteSweepline
R11 DeleteSweepline ->
SelectSpacer
R8 DragBox SelectSpacer -> DragSpacer
R12 SelectSpacer
-> DeleteSpacer
Discrimination. Rule R10's context is the failure to solve DragToBoxTop's constraints. After deleting the sweepline, Pam picks the spacer. This matches the context of rule R8, SelectSpacer. Metamouse predicts DragSpacer, but never displays this to the user because it would have no effect (it's already to the right of the last box sorted). When Pam deletes the spacer, it has to fix the rules so that SelectSpacer leads to DragSpacer or DeleteSpacer as appropriate. Metamouse keeps rules deterministic by specializing them, which means lengthening their context, specializing only as much as necessary to prevent conflict. It tries to lengthen the older rule first (based on the weak heuristic that if several events consistently follow one another over many iterations, they form a reliable context). Hence it changes the context of R8 to (DragBox SelectSpacer), which always predicted DragSpacer and does not predict DeleteSpacer. If no specialization covers all examples (for instance, if in one iteration GrowBox rather than DragBox preceded SelectSpacer) then Metamouse specializes the new rule instead. In that case, R12 would be (DeleteSweepline SelectSpacer) -> DeleteSpacer. There is always at least one context that could distinguish a new rule from any older rule, namely the entire preceding history trace.
When the user rejects a prediction and demonstrates a new action, Metamouse specializes the old or new rule, as outlined above, so that it would predict only the new action in the current context. Rule specialization finesses the issue of debugging, by reducing though not eliminating the chance that a bad rule fires. It avoids asking the user whether an action should be deleted entirely, or is inappropriate in the current state of the procedure, or depends on a conditional test that Basil cannot learn. A buggy rule may fire again, in particular when its context is the entire preceding trace and the procedure is re-started. In this case it is reasonable for Metamouse to identify the rule as a bug and delete it.
A loop is a subset of the rules that when traced forms a circuit. Metamouse can learn loops that repeatedly visit objects, draw a fixed number of new ones, or scan through a set of similar ones. Metamouse equates set iteration with search: set iteration is based on having "find" selectors in constraints that bind variables differently on each iteration. Metamouse infers a find selector only when it meets an object for the first time (if Basil had touched it before, the selector is "value unchanged"); therefore Metamouse cannot infer a set iteration over objects used earlier in the same task. This is unfortunate, since people naturally break tasks down into subtasks done in several passes over the same things. For instance, if Pam wanted to sort a group of boxes not initially aligned, she would have to do the aligning and sorting as two separate tasks, rather than two loops in one task.
To alleviate this problem, Metamouse will need to revise "value unchanged" to "find" when multiple examples or user command warrant. A "re-process set" selector choosing objects from a variable's history stack would also help it learn to pair one loop with another, or one object with another. For instance, if the user has a set of boxes connected to lines, then moves the boxes, she may want to reconnect the lines later on, which means that Basil must have some way of remembering which line goes with which box.
Conditionals are based on postconditions; Metamouse does not represent preconditions. Metamouse can learn to branch when some action's constraints are insoluble, as when exiting the sorting task loop. The ramifications of branching only on postconditions are subtle, because some factors that might seem to be preconditions (such as the existence of a box when searching for a one) are accounted for by postconditions (if there is no box, the "find" selector fails and the action is not predicted). Moreover, one step's postcondition is effectively a precondition on subsequent steps. But it may happen that special cases of a postcondition determine subsequent branching, which Metamouse does not capture.
A repeated non-looping sequence is a group of rules entered from and exiting to several different chains of rules. It resembles a subroutine but lacks the abstraction normally achieved in hierarchical grammars by substituting a single symbol for the subsequence. Exits to different chains are represented by rules whose context begins with an action from the chain and includes the entire subsequence. Thus, if the subsequence contains any branching structures, Metamouse must learn a separate exit rule for each path.
We asked our users to perform six tasks at least three times each: first without Basil's help, then with it, and once again without. We compared the times to complete the second and third runs, so that practice effects would bias against Metamouse rather than for it. We allowed users more than one practice run without Basil, so that they would understand the task, and more than one trial with Basil--perforce because the program often crashed! A facilitator (who knew nothing of the system's internal workings) helped subjects learn the tasks but did not advise them on how to teach Basil.
Subjects. We wanted subjects representing a variety of potential Metamouse users: drafters who would find constructions quite natural; graphic designers who would be accustomed to measuring by eye; non-graphic computer users who would find the techniques utterly novel; and computer programmers who would have algorithmic insights. In the event, we did a small study with one graphic designer, three programmers and three geologists. The geologists interested us because they had no experience of drawing programs and years of work in contour mapping, which biased them against using constructions--they had no trouble aligning and spacing objects almost perfectly by eye.
Tasks. The six tasks are illustrated in Figure 6. All subjects worked with the data shown in the panels. Users can easily accomplish the first two tasks without construction tools, so they get a feel for working with a predictive interface. The middle two are rather difficult, the last two are easier.
Task 1: Squeeze and align. Figure 6a. For each group of boxes, the user must squeeze the middle one and move the rightmost so that all align at the bottom. No extra objects need be created to construct this relationship. Basil can predict all steps after the user repeats one selection (for instance, after the user picks the second box, Basil will move it into place and continue with the third box).
Task 2: Pancaker. Figure 6b. A variant of task 1, the middle box is squeezed and the rightmost is moved up and squeezed so all three are the same height. Comments: To illustrate the "generality" of Basil's constraint inference, the third box in the last group must be "unsqueezed" since it is too thin. No extra objects required. Basil can predict all edits to the second and third groups.
Task 3: Picket fence. Figure 6c. The user must space all boxes evenly, keeping them aligned at the bottom. The user must create a construction line or box to indicate the desired gap between them, since locations and distances moved vary from one example to the next. Ideally, Basil can start predicting on the second or third box.
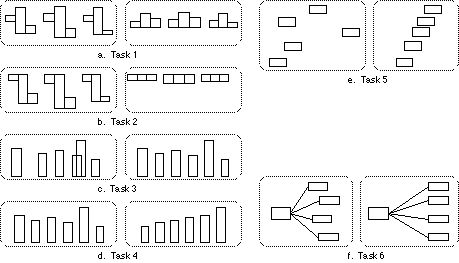
Task 4: Sort by height. Figure 6d. The user must sort the boxes so they increase in height from left to right, remaining aligned and evenly spaced. Without using a sweepline, the user may need to give two examples before Basil generalizes the heading to upwards (moving to the tallest box could be mostly rightwards, and to the next tallest, leftwards). Ideally, Basil can sort five of the six boxes. The spacing/alignment subtask is a repeat of Task 3, but since Metamouse cannot infer two loops over the same set of objects, the user must combine spacing, alignment and sorting into one loop.
Task 5: Stairway. Figure 6e. The user must align the boxes' lower right corners to an arbitrary guide. This requires a line as an input to the procedure. The user may select boxes in any order, but then Basil may infer a heading such as "left" or "right". Should this happen, it may not find all the remaining boxes until the user gives examples that cause it to generalize the path to "any direction."
Task 6: Organization chart. Figure 6f. Given a set of boxes all connected by tie-lines to one other box, the user moves them into alignment at the right, and reconnects the tie-lines. A guideline is required as in Task 5. For Basil to predict editing the tie-lines, the user's procedure must form a single loop (drag-box, drag-tie-line)*, as opposed to (drag-box)* (drag-tie-line)*.
Construction. We expected that users would make appropriate construction tools after reading the manual and watching Basil fail once or twice to infer a spatial relation. Most users (especially programmers) expected Basil to find simple relations like constant spacing or alignment of edges, despite what the manual said, but they immediately understood its failure on their first attempt to teach Task 3. After that, all but one consistently anticipated the need to construct spatial relations, even when they aligned or spaced by eye during practice.
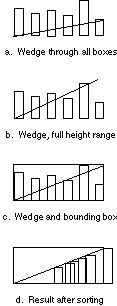
Users made tools as analogs of spatial relations (e.g. a line for alignment, a box as a spacer between boxes), but had little or no success inventing dynamic, procedural constructions (such as a sweepline to pick boxes in height order). Generally, non-programmers gave better explanations of why their tools failed; programmers tried to second-guess the implementation. Only one subject (a programmer) made a moving tool (a sweepline for Task 5). Only one subject (a geologist) invented a useful tool for Task 3 (see Figure 7). Users immediately made tools for alignment but had to think about spacing. Some tried tools that merely hinted at a relation: in Task 3 for instance, one person drew a horizontal line through all boxes to suggest horizontal spacing.
Set iteration. As mentioned above, Metamouse cannot infer a set iteration until it comes across an object it has not previously met. This restriction is both unreasonable and inconsistent (only the first thing processed by the loop need be unfamiliar, the rest may have been touched before). We believed that users would have no insight into this problem, nor even recognize it, and we found that any failure to form a loop utterly confused them. Based on their comments, they assumed Basil could iterate over all objects of the same type, all objects touching a particular one, and all objects forming a structure.
People have two ways of decomposing iterations over sets of objects with multiple parts [van Sommers 84]: repeat for all objects (edit all parts of one object, then another); and repeat for all parts (edit all instances of one part, then another, and so on). Metamouse learns "repeat for all objects" only, but with few exceptions our users tried to teach "repeat for all parts". One user did surmise that Basil "cannot remember which parts go with which" in Task 6.
An unfortunate side-effect of the loop restriction is the way it punished users for their efforts in making constructions. For instance, the wedge tool in Figure 7 actually prevented automation. Because the line passed through most boxes when it was first drawn, Basil could not learn to select them iteratively: each demonstration presented an object already encountered in that preliminary step.
Scanning. We predicted that users would teach Basil to scan along an axis for the next object, as illustrated in the manual. We found in Tasks 5 and 6 that users often selected the nearest object rather than the next one along an axis. They might begin with the rightmost box, move it to the guideline and then pick the box immediately above it. They assumed nonetheless that Basil would iterate in order over the entire set. Our subjects did not use sweeplines, nor transfer the notion of scanning to other applications like sorting by height.
Intrinsic properties. We predicted that users would expect Basil to infer properties like height. None of the subjects believed Basil knew about height. All puzzled over how to teach it to sort, because they believed they were supposed to find some way of expressing height in terms of touch and thought this impossible. Several users said they would rather give verbal commands to specify properties and relations.
Eager prediction. We expected that users would want Basil to predict as soon as possible. In fact, no one complained about its eagerness, and few about its mistakes. We suppose that they were more concerned with the trouble they had inventing constructions. Complaints concerned Basil's failure to predict.
General observations. Users related well to the turtle and believed it helped them understand and remember Basil's characteristics. They expected the system to learn from one example but also to continue generalizing as it encountered more. They believed it would remember incorrect actions but would not predict them after being taught a correction. None (including programmers) wanted to see printed listings of procedures learned. Most people said they would use an agent like Metamouse, provided it could learn from its mistakes (multiple examples) and take direct verbal instructions.
The general conclusion we drew from the study is that graphical constructions, though useful, should not be the sole basis of teaching, since few people have strong intuitions about them. The system should infer spatial relations from multiple examples, provide tools for teaching and take verbal instructions.
Eager (Chapter 9) and Metamouse both predict patterns over history. Eager finds looping patterns; Metamouse also finds branching ones. Metamouse is more eager than Eager, which waits for two or three repetitions of an entire sequence before predicting. Metamouse justifies prediction by requiring a strict match of all features chosen by its generalization rules. Eager is less strict (it generalizes by choosing one repeated feature somewhat arbitrarily), but its repertoire of generalizations reflects the considerable domain knowledge of application designers. On the whole, one would expect Eager to make better predictions, but occasionally miss loops due to accidental variation in actions.
TELS (Chapter 8) adopts a strategy like Mondrian's: the user initiates generalization by re-invoking a straight-line procedure on new data. This provides justification for generalizing search patterns over multiple examples, which Metamouse cannot do. Tels also specializes patterns, by storing negative examples on an exceptions list. It does not form conditional branches, however.
Chimera (Chapter 12) infers constraints from multiple examples, using candidate elimination [Mitchell 82] to isolate invariants. Metamouse infers only constraints that result from actions--touch relations that change. But the user can make an invariant touch into a constraint, by clicking on its tack.
Peridot (Chapter 6) and Lapidary (Chapter 10) include many special purpose constraints that make them more efficient than Metamouse for specifying relations. Metamouse is arguably more extensible because its construction approach allows for open-ended invention.
Although Triggers (Chapter 17) is not inference-based, it includes techniques and devices useful in teaching an agent like Metamouse. Of particular relevance are a search window indicating where to look relative to current position, and markers placed on objects or locations that should be remembered.
Other systems. Among the systems for programming by demonstration omitted from this book, those most closely related to Metamouse are Noddy [Andreae 85], Office Clerk [MacDonald 87] and ETAR [Heise 89]. All three, like Metamouse, use a sensory focus of attention centered on the agent being taught. Noddy, like Basil, has a fixed built-in focus. The Office Clerk observes something only when the user explicitly tells it to. ETAR does both automatic and manual focusing: it dynamically focuses on objects lying nearest its robot arm, but also lets the user specify the objects used in a task (like parameters in a Mondrian macro). When the objects in the dynamic focus match on two different occasions, ETAR checks for a loop. When sequences mismatch, ETAR looks for differences between their sets of focus objects to use as a conditional test.
The Metamouse approach to PBD is to create the illusion of teaching an agent with limited sensory abilities and ostensibly no task knowledge. The user can specify constraints by graphical construction, so that open-ended programming is possible. By interacting with the agent, the user can override its inferences without leaving a graphics-oriented, direct-manipulation mode of work.
Metamouse generalizes individual actions from a single example. It infers constraints on the location to which the mouse cursor (and anything attached to it) should move after each editing step. Constraints are touch relations, direction, distance and position. It infers variables and functions to set their values by creating, searching for or re-using objects. Like most PBD systems, Metamouse takes a knowledge-intensive approach to generalizing actions. In contrast, it infers program structure by purely syntactic matching of multiple examples, both positive and negative. The learning algorithm infers a procedure in the form of production rules whose contexts are previous actions. Because the contexts are variable-length, the ruleset can emulate any deterministic finite state machine.
Metamouse matches actions and predicts at the first opportunity. This eagerness helps users in four ways. First, they reap early benefits when performing repetitive operations. Second, they can detect and correct errors immediately. Third, accidental variation in the ordering of steps or the method used (which might prevent the matching of sequences) is avoided. Fourth, users develop confidence in their programs without ever viewing any kind of listing.
Some flaws in the system design compromise its effectiveness. In particular, it cannot use multiple examples to refine hypotheses about which constraints are relevant or which functions should be used to set variables. Although the user can demonstrate new actions to correct mistakes, Metamouse does not necessarily learn from them because its rules may infer the same incorrect generalization as before. Another serious shortcoming is its inability to learn iterations over objects encountered previously during a task; hence it often fails to find repetitions that users consider obvious.
The second question is hard to put in testable form. We took "easily taught" to mean that average computer users with minimal training on the system could devise appropriate demonstrations with little planning or revision. We tested contrasting groups of users (geologists and programmers) on a variety of tasks that exercised all the system's inference abilities. We were looking for advantages that one group might have over another, and for special difficulties that some tasks might present. Our user study showed the major difficulty was the hard limit on learnability described above, but the class of easily taught tasks may be smaller still, because users found it unnatural to think about all spatial relations in terms of constructed touch. One might argue however that we went overboard on "minimal training" (a one-page manual and less than 10 minutes experience before subjects encountered the two hardest tasks).
The fulcrum of teachability is the metaphor, which encourages users to invent their own way of teaching, yet be aware of the system's limitations. Metamouse's learning system needs some improvements before an easily understood metaphor could represent it reliably. In particular we propose (a) a more general model of sets, (b) the ability to revise any generalization, (c) inference of other spatial relations (relative size, distance, alignment, inside and outside), and (d) the potential to output and input verbal descriptions.
Finally, a word about implementation. Metamouse is a complicated program. The current version consists of 11k lines of documented C++. The core of the learning system is only 1k lines, but its interface to the application includes a constraint solver (1k lines) and code for accessing state (2k lines). We observed with regret that our users encountered many bugs we had missed. The difficulty of building and repairing such a system justifies extensive use of simulated prototypes, which has led to the Turvy methodology described in Chapter 11.
Metamouse has helped us explore the issues that arise when putting a machine learning system to work in a user interface. Its failings shed light on sources of difficulty when human and computer agents having markedly different conceptual frameworks try to cooperate. Its successes give us reason to believe that a truly instructible interface is possible, given a suitable model of computation, a learning engine with restricted but flexible focus, and methods of instruction that keep users in their own framework yet give them carefully guided and mediated access to the computer's. We look forward to working with Basil's progeny.

Intended users: Non-programmers
Feedback about capabilities and inferences:
Metamouse displays black tacks to show intersections that it guesses are significant. Metamouse asks the user to confirm each action while it is performing the task in the learning phase, by clicking yes or no in a dialog box.
Types of examples: Metamouse generalizes individual actions from single examples, and loops and branches from multiple examples.
Program constructs: Variables, iteration, conditionals.
 Table of Contents
Table of Contents  Watch What I Do
Watch What I Do