"Watch What I Do" Chapter 13


Chapter
13

The Geometer's Sketchpad:
Programming by Geometry

R. Nicholas Jackiw
and
William F. Finzer

Introduction

Think about relationships: "Clark is a friend of Janet," "The picture is fastened to the wall," "Mount Mitchell is one hundred feet higher than Clingman's Dome." Knowledge of relationships is a key to problem solving. Providing knowledge of relationships to a computer learning environment enables the computer to become an effective partner in the problem solving process. Central issues in the design of such environments involve how we inform the computer of relationships relevant to the problem at hand, and how the computer exploits these relationships.

A particular problem solving domain is considered here -- Euclidean geometry. In this domain, the objects of concern are points, lines, and circles, and relationships in this realm are spatial; for example, "perpendicular to," "at the intersection of," and "with radius equal to." We explore the process of expressing geometric relationships visually and by demonstration. We call this process "sketching" and develop through it a notion of "spatial programming."

The specific application considered here is The Geometer's Sketchpad[1], an environment for exploring geometry now being used in thousands of high school mathematics classrooms. The primary purpose of GSP's ongoing development is the resolution of real-world issues surrounding the learning of geometry. It is surprising to find that this practical focus leads to a theoretically interesting conception of users programming by demonstration. Because in GSP there is no distinction between the geometric content domain and the spatial programming domain, students using it encounter programming as the central activity. The distinction between programmer and user disappears; the two coalesce into one -- the student.


The Geometer's Sketchpad

Uses and Users

Application domain: Euclidean geometry

Intended users: Students

User Interaction

How does the user create, execute and modify programs?
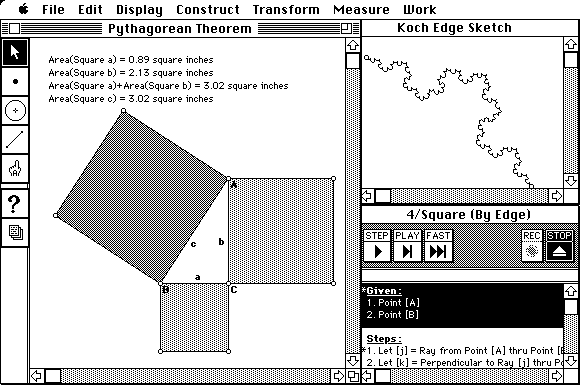
The user creates a program by making a geometric construction. It is also possible to turn on a recording mode and give an example of a geometric construction, which can then be replayed in the context of different objects.
Programs are debugged by dragging objects into different configurations to test their behavior for different "inputs". Constraints can be added or removed at any time.

Inference

Program constructs: Variables, procedures with parameters, recursion

Knowledge

Types and sources of information:
Knowledge about geometry. For instance, lines, rays, and line segments are all "straight objects".

Implementation

Machine, language, size, date: 1991.

back to ... Table of Contents Watch What I Do